
Official Project-Website

|
(IST project IST-FET-2001-37004) Official Project-Website |
DLVK
The
DLVK-system
is based on the logic-based planning language
K which - unlike previously proposed languages of this kind -
is well-suited for representing incomplete knowledge.
This languages provides a number of convenient features, for instance
to specify the degree of security for plans in nondeterministic domains,
or action costs which allow to seek for optimal plans.
The
DLVK-system
has been implemented on top of the underlying ASP-system
DLV.
In what follows, we present the basic componentes in specifying a planning problem, on an example from the blocks world. We identify the description of a planning problem as
A general description of the planning domain (background-knowledge)
which describes general effects of actions.
Example: "If one puts a block
from the table onto another block, it is not on the table anymore".
For an example, including other such statements see the input-file
blocksworld.plan.
A description of the actual domain.
Example: "There are
blocks a, b, c and a table
t".
See blocksworld_inst.dom.
A specification for the desired plan, containing an initial state and
the desired goal state. For example:
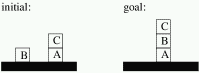
Represented by an input file
blocksworld_inst.plan.
Now
run the example with DLVK.
The usage of ASP is inherent in the approach of DLVK
since this system is based on an appropriate transformation from planning
problems into a logic program, which is then evaluated with ASP-systems.
As was early recognized, logical formulations of planning problem have to face the so-called frame-problem, which, roughly speaking, refers to the fact that each item in the environment unaffected by an action, remains unchanged. Using classical logics for planning one needs to formalize this set of default assumptions in an explicit manner, which is an obstacle from both a theoretical and practical point of view. The use of the negation-as-failure operator in ASP allows for a much more elegant way to deal with the frame-problem. Moreover, exploiting ASP-features extends the scope of planning to, e.g.,
DLVK-programs consisting of three parts
(as sketched above), namely
the background knowledge (file.plan),
the domain description (file_inst.dom),
and the plan description (file_inst.plan) for several
showcase problems.
For each of the problems, the actual input files
can be browsed via the "View Example"-link. The "Run Example"-link
runs the DLVK-system in real-time with
the provided files and gives the output of the system, which is
to be understood as a list of optional plans.
The classical Traveling Salesperson Problem (TSP) seeks for the
most economical (wrt to the cost from one city to another) trip visiting
all considered cities. The
DLVK-feature of action costs allows for a
simple representation of TSP by means of a planning problem. Moreover,
the example shows that the extension of TSP to exceptional costs, which
hold only at a certain timepoint, is easy to represent in DLVK.
Our examples considers a TSP where we want to visit all
capitals of the nine Austrian federal states (click on graphic to enlarge).
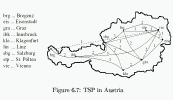
The costs of the connections is given in travelling hours and
represented in the domain description (see files below).
Assume that we only make a single trip per day,
and we assign an extra cost for the trip from St.Pölten to
Eisenstadt on Tuesday (see domain description).
We start our tour in Vienna, and seek for a tour (a plan)
in 8 days with minimal costs as specified in the plan specification.
Finally, the description of the planning domain basically provides
a single action travel(X,Y) which marks cities after
being visited and cumulates the cost; the mark for being visited is
the only inertial.
Consider a number of person wants to cross a river at night over a plank bridge, which can only hold up two persons a time. They have a lamp, which must be used when crossing. As it is pitch-dark and some planks are missing someone must bring the lamp back to the others; no tricks like throwing the lamp are allowed. Moreover, the persons need different different times to cross the bridge, and walking in two implies slower speed.
Consider four persons, Joe, Jack, William, Averall with different
walking speeds of 1, 2, 5, and 10 minutes respectively.

Is it possible for them to reach the other riverbank in less than 20 minutes?
Is it possible for them to reach the other riverbank in less than 19 minutes? Yes, if we allow plans with more than 5 steps:
View Example; Run Example (takes some more time).
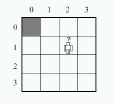
This problem is about self-location of a robot which moves in a wall-bounded n x n - grid. The robot can move in four directions (up, down, left, right) and does not know its initial position. The problem of finding a conformant plan for reaching a fixed position is known as the SQUARE(n) problem, and is not solvable by traditional planning system, since the inital state is incompletely defined.
In our concrete example we use a 4 x 4 - grid and also allow
diagonal moves.
Project-Homepage:
DLVK-system
(with further examples and system download).
Literature:
[1]
describes the DLVK-system in detail;
[2] addresses semantics and complexity of the language K;
and [3] discusses the feature of action costs.
An overview on all aspects of DLVK can be found in
[4] and in the
PhD-Thesis
by
Axel Polleres [5].
page mainted by Stefan Woltran; graphics and examples provided by Axel Polleres.