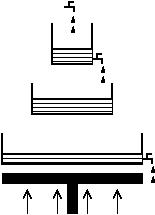

Consider three containers, small, medium, and large, for storing water. The small container is suspended over the medium, and the medium container is suspended over the large so that, when the small (resp. medium) container is full of water, the water poured into the small (resp. medium) container overflows into the medium (resp. large) container. Suppose that there are three taps: one directly above the small container, by which some water can be added to the containers from an external source, one on the small container, by which some water can be released into the medium container, and a third tap on the large container to release water to the exterior. Suppose also that one unit increase (resp. decrease) of water in the large container increases (resp. decreases) the amount of force applied downwards to the bottom of the large container by two units. Also assume that some force is exerted upwards at the bottom of the large container, e.g., by a piston, to lift it up.
Suppose that the small, medium, and large containers can contain at most 2, 3, and 4 units of water respectively; and that the amount of the force applied upwards at the bottom can be at least -8 and at most 8. Initially, each container has 1 unit of water, and the amount of force applied is -2. How much water will there be in each container, and what will be the total amount of force applied upwards at the bottom of the large container, after concurrently adding 8 units of water into the small container, releasing 1 unit of water from the small container, releasing 2 units of water from the large container, and exerting 8 units of force upwarsd by the piston?
Here are some formalizations of the containers domain:
Here is a formulation of the prediction problem above:
To compute a solution to this problem using ccalc, you need the modified source files ccalc-cr.pl and additive-cr. To compute a solution using a golog interpreter, you need the file additive-cr.pl.