Glossary
Default Logic Simulation - Online-Help 
This applet should visualize the method for finding extensions
of a given default theory (comprising definite knowledge
plus a number of default assumptions) presented in the lecture "Wissensbasierte
Systeme" at the TU Vienna. This lecture
is obligatory for students of computer science.
System requirements:
For running this applet all you need is a Java 1.1 capable browser, e.g.
Netscape 4.06 or higher. We have tested it under Solaris and Windows95/NT
using Netscape.
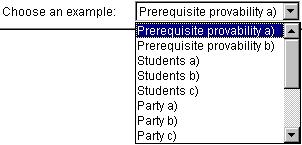
Description of the applet: After loading you can choose an example
from a list (partly examples from the lecture, partly taken from old exams):
By clicking the button  you can open this Help-Site.
you can open this Help-Site.
After you have selected an example, the sets W (the initial knowledge)
and D (a set of Defaults), which represent the chosen
default
theory, are shown.
The button  remains
inactive until you have chosen an example. Clicking this button you get
a short description of the selected example.
remains
inactive until you have chosen an example. Clicking this button you get
a short description of the selected example.
The button  also remains
inacative until you select an example, it opens the simulation
window, which shows how candidates for extensions are calculated.
also remains
inacative until you select an example, it opens the simulation
window, which shows how candidates for extensions are calculated.
After the candidates for extensions have been calculated, a table showing
the list of candidates to be tested is displayed in the applet window,
e.g.:

You can select one of the canditates for testing either by selecting
it in this list  or by simply clicking on it in the table. The testing of a candidate is
again shown in an own simulation window, that
visualizes how you can check if a candidate really is an extension or not.
or by simply clicking on it in the table. The testing of a candidate is
again shown in an own simulation window, that
visualizes how you can check if a candidate really is an extension or not.
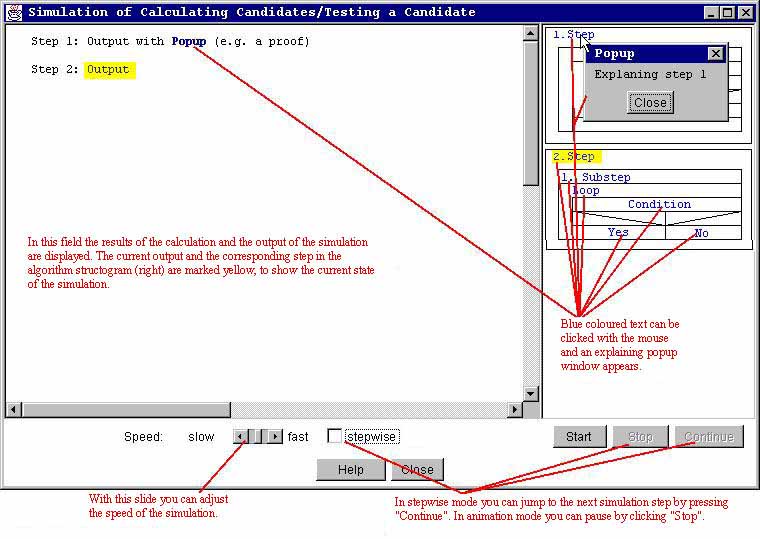
Simulation window
The calculation of possible candidates and testing of a single candidate
is shown in an own window. Here you can see the most important elements
of the user interface:
Glossary
-
Consequent: the conclusion of a default.
-
DS : refer to classical
reduct.
-
Default: a default is a classical inference rule plus a set
of consistency conditions, which allows you to model rules that are "normally"
true, that is, as long as the consistency condidtions are not violated.
A Default consists of three parts, the prerequisite, a
set of justifications (consistency condiditons) and the consequent
(conclusion).
Formal definition: Let A(X), B1(X), B2(X), ...,
Bn(X), C(X) be first order formulas, with X = (x1,
x2, ..., xn) being the set of free variables occuring
in these formulas. Then a Default is an expression of the form:
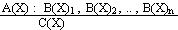 A(X)
... prerequisite
A(X)
... prerequisite
{ B1(X), B2(X), ..., Bn(X)}
... consistency conditions ( = justifications)
C(X)
... consequent, conclusion
The Default 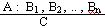 for example can be read as follows: "If A is valid and there are no objections
to B1, B2, ..., Bn , then C.
for example can be read as follows: "If A is valid and there are no objections
to B1, B2, ..., Bn , then C.
-
Default theory: a default theory T=(W,D) is an
ordered pair, where W is a set of closed formulas and D is a set of defaults.
W represents the premises of T, that means the initial knowledge
("hard facts"). D represents relations that are normally valid.
-
Extension: The extension of a default theory (W,D) is intuitively
spoken one possible world which emerges from the initial knowledge when
applying a maximum number of defaults, that don't "block" themselves or
each other.
Formal definition (Reiter 1980):
Let T = (W,D) be a (closed) Default Theory
1) We define an operator 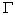 T
as follows:
T
as follows:
Let S be a set of closed formulas. Then 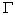 T(S)
is the smallest set that fulfills the following conditions:
T(S)
is the smallest set that fulfills the following conditions:
DT1(S): K = Th(K)
... that means K is its deductive closure.
DT2(S): W is a subset of K.
DT3(S): If 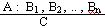
 D
and A
D
and A 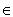 K and
K and 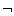 B1,
B1, 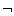 B2,
...,
B2,
..., 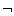 Bn
Bn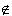 S, then C
S, then C 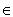 K.
K.
2) A set E of closed formulas is an extension of T iff 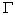 T(E)
= E, that means E is a fixed point of
T(E)
= E, that means E is a fixed point of 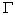 T.
T.
-
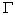 -Operator (read
"Gamma-Operator"):
refer to
Extension (
-Operator (read
"Gamma-Operator"):
refer to
Extension (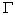 T)
T)
-
Justifications: The justifications represent consistency
conditions, that means if you want to apply a default, all justifications
have to be satisfied.
-
classical Reduct: Let S be a set of closed formulas (in this
special case a candidate for an extension) and let D be a set of (closed)
defaults. The classical reduct of D with respect to S is the following
set:
DS = {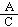 |
| 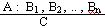
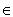 D,
D, 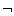 B1,
B1,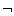 B2,...,
B2,...,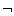 Bn
Bn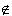 S
}
S
}
The classical reduct is a set of residues.
-
Minimality/maximality of extensions: Let E, F be extensions
of a default theory T=(W,D), then E
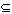 F always implies that E = F.
F always implies that E = F.
-
normal: A default of the form
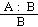 is called normal; a default theory, where all defaults in D are
normal is called normal default theory. Each (closed) normal default
theory has at least one extension!
is called normal; a default theory, where all defaults in D are
normal is called normal default theory. Each (closed) normal default
theory has at least one extension!
-
Prerequisite: the precondition for applying a default. A
default with only a prerequisite but no justifications is very similar
to a classical inference rule.
-
residue: the residue of a default
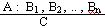 is the classical inference rule
is the classical inference rule 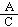 .
.
-
seminormal: A default of the form
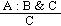 is called seminormal; a default theory where all defaults in D are
seminormal is called seminormal default theory. With seminormal
defaults you can encode priorities.
is called seminormal; a default theory where all defaults in D are
seminormal is called seminormal default theory. With seminormal
defaults you can encode priorities.
-
Th(W): The deductive closure of a set W, that means
all formulas that can be classically derived from W, e.g. using resolution.
-
ThDs(W): Let S be a closed set and T=(W,D) a default
theory, then ThDs(W) is the set of all formulas, which can be
classically derived from W by using in addition the rules in the classical
reduct DS.
The set ThDs(W) equals 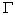 T(S)
!!!! Since each fixed point of
T(S)
!!!! Since each fixed point of 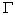 T(S)
represents an extension, S is an extension of the default theory T = (W,D)
iff
ThDs(W) = S
The tests of the respective candidates in our applet are based on this
concept, as you will find out when studying the simulations!
T(S)
represents an extension, S is an extension of the default theory T = (W,D)
iff
ThDs(W) = S
The tests of the respective candidates in our applet are based on this
concept, as you will find out when studying the simulations!
you can open this Help-Site.
remains
inactive until you have chosen an example. Clicking this button you get
a short description of the selected example.
also remains
inacative until you select an example, it opens the simulation
window, which shows how candidates for extensions are calculated.
or by simply clicking on it in the table. The testing of a candidate is
again shown in an own simulation window, that
visualizes how you can check if a candidate really is an extension or not.
for example can be read as follows: "If A is valid and there are no objections
to B1, B2, ..., Bn , then C.